0803 空间直线、平面的平行:修订间差异
| (未显示同一用户的10个中间版本) | |||
| 第30行: | 第30行: | ||
(2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积. | (2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积. | ||
| 第66行: | 第68行: | ||
===3、2019江苏,16=== | ===3、2019江苏,16=== | ||
[[文件:2024051403.png|缩略图|右]] | [[文件:2024051403.png|缩略图|右]] | ||
如图,在直三棱柱$ABC-A_1B_1C_1$中,$D,E$分别是$BC,AC$的中点,$AB=BC$. 求证: | |||
(1)$A_1B_1\parallel$平面$DEC_1$; | (1)$A_1B_1\parallel$平面$DEC_1$; | ||
(2)$BE\perp C_1E$. | (2)$BE\perp C_1E$. | ||
| 第92行: | 第96行: | ||
(2)求二面角$A-MA_1-N$的正弦值. | (2)求二面角$A-MA_1-N$的正弦值. | ||
2024年6月13日 (四) 14:51的最新版本
知识要点
例题
1、2021浙江,6
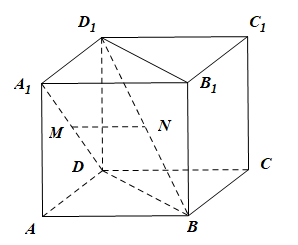
如图,已知正方体$ABCD-A_1B_1C_1D_1$,$M,N$分别是$A_1D,D_1B$的中点,则$(\qquad)$
A. 直线$A_1D$与直线$D_1B$垂直,直线$MN\parallel$平面$ABCD$
B. 直线$A_1D$与直线$D_1B$平行,直线$MN\perp$平面$ABCD$
C. 直线$A_1D$与直线$D_1B$相交,直线$MN\parallel$平面$ABCD$
D. 直线$A_1D$与直线$D_1B$异面,直线$MN\perp$平面$ABCD$
2、2023全国乙文,19
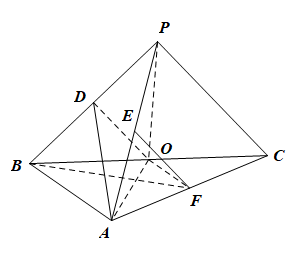
如图,在三棱锥$P-ABC$中,$AB\perp BC$,$AB=2$,$BC=2\sqrt{2}$,$PB=PC=\sqrt{6}$,$BP,AP,BC$的中点分别为$D,E,O$,点$F$在$AC$上,$BF\perp AO$.
(1)证明:$EF\parallel$平面$ADO$;
(2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积.
练习
1、2019课标Ⅱ,7
设$\alpha,\beta$为两个平面,则$\alpha\parallel\beta$的充要条件是$(\qquad)$
A. $\alpha$内有无数条直线与$\beta$平行
B. $\alpha$内有两条相交直线与$\beta$平行
C. $\alpha,\beta$平行于同一条直线
D. $\alpha,\beta$垂直于同一平面
2、2022全国乙理,7
在正方体$ABCD-A_1B_1C_1D_1$中,$E,F$分别为$AB,BC$的中点,则$(\qquad)$
A. 平面$B_1EF\perp$平面$BDD_1$
B. 平面$B_1EF\perp$平面$A_1BD$
C. 平面$B_1EF\parallel$平面$A_1AC$
D. 平面$B_1EF\parallel$平面$A_1C_1D$
3、2019江苏,16
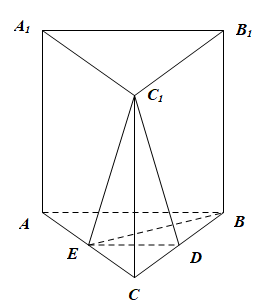
如图,在直三棱柱$ABC-A_1B_1C_1$中,$D,E$分别是$BC,AC$的中点,$AB=BC$. 求证:
(1)$A_1B_1\parallel$平面$DEC_1$;
(2)$BE\perp C_1E$.
4、2019课标Ⅰ理,18
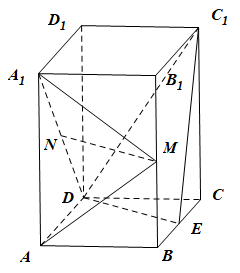
如图,直四棱柱$ABCD-A_1B_1C_1D_1$的底面是菱形,$AA_1=4$,$AB=2$,$\angle BAD=60^\circ$,$E,M,N$分别是$BC,BB_1,A_1D$的中点.
(1)证明:$MN\parallel$平面$C_1DE$;
(2)求二面角$A-MA_1-N$的正弦值.