7.2 离散型随机变量及其分布列:修订间差异
来自高中数学
(→例题) |
(→例题) |
||
| (未显示同一用户的3个中间版本) | |||
| 第11行: | 第11行: | ||
(2)$p_1+p_2+\cdots+p_n=1$. | (2)$p_1+p_2+\cdots+p_n=1$. | ||
* 两点分布 | * 两点分布 | ||
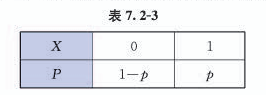
如果$X$的分布列如表7.2-3所示: | 对于只有两个可能结果的随机试验,用$A$表示“成功”,$\bar{A}$表示“失败”,定义$$X=\begin{cases}1,A发生,\\0,\bar{A}发生.\end{cases}$$ | ||
如果$P(A)=p$,则$P(\bar{A})=1-p$,那么$X$的分布列如表7.2-3所示: | |||
[[文件:2024040801.png]] | [[文件:2024040801.png]] | ||
| 第18行: | 第19行: | ||
==例题== | ==例题== | ||
例1 | 例1 一批产品中次品率为$5\%$,随机抽取1件,定义$$X=\begin{cases}1,&抽到次品,\\0,&抽到正品.\end{cases}$$求$X$的分布列. | ||
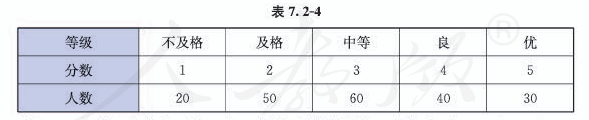
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每天个等级对应的分数和人数如表7.2-4所示. | 例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每天个等级对应的分数和人数如表7.2-4所示. | ||
[[文件:2024040802.png]] | [[文件:2024040802.png]] | ||
从这200名学生中任取1人,求所选同学分数$X$的分布列,以及$P(X\geqslant4)$. | 从这200名学生中任取1人,求所选同学分数$X$的分布列,以及$P(X\geqslant4)$. | ||
例3 一批笔记本电脑共有10台,其中A品牌3台,B品牌7台. 如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列. | |||
==练习== | ==练习== | ||
2024年7月27日 (六) 10:24的最新版本
知识要点
- 随机变量
一般地,对于随机试验样本空间$\Omega$中的每个样本点$\omega$,都有唯一的实数$X(\omega)$与之对应,我们称$X$为随机变量. 可能取值为有限个或可以一一列举的随机变量,我们称之为离散型随机变量.
- 概率分布列
一般地,设离散型随机变量$X$的可能取值为$x_1,x_2,\cdots,x_n$,我们称$X$取每一个值$x_i$的概率$$P(X=x_i)=p_i,i=1,2,\cdots,n$$为$X$的概率分布列,简称分布列.
根据概率的性质,离散型随机变量分布列具有下述两个性质:
(1)$p_i\geqslant0,i=1,2,\cdots,n$;
(2)$p_1+p_2+\cdots+p_n=1$.
- 两点分布
对于只有两个可能结果的随机试验,用$A$表示“成功”,$\bar{A}$表示“失败”,定义$$X=\begin{cases}1,A发生,\\0,\bar{A}发生.\end{cases}$$ 如果$P(A)=p$,则$P(\bar{A})=1-p$,那么$X$的分布列如表7.2-3所示:
我们称$X$服从两点分布或0-1分布.
例题
例1 一批产品中次品率为$5\%$,随机抽取1件,定义$$X=\begin{cases}1,&抽到次品,\\0,&抽到正品.\end{cases}$$求$X$的分布列.
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每天个等级对应的分数和人数如表7.2-4所示.
从这200名学生中任取1人,求所选同学分数$X$的分布列,以及$P(X\geqslant4)$.
例3 一批笔记本电脑共有10台,其中A品牌3台,B品牌7台. 如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.