必修一问题讨论

这是一个专门用来讨论必修第一册问题的页面，点讨论进入，点页面回来。

讨论从新建一个话题开始

• 先看一下范例：帮助
• 点击新建话题，为了浏览的方便，一定要写一个主题
• 正事说完了，最好换一行，并输入两个减号--

三角练习题

1.

已知$\dfrac{\pi}{4}<\alpha<\dfrac{3\pi}{4}$，$\sin(\dfrac{\pi}{4}-\alpha)=-\dfrac{1}{2}$.

（1）求$\cos\alpha$的值；

（2）若$0<\beta<\dfrac{\pi}{4}$，$\cos(\dfrac{\pi}{4}+\beta)=\dfrac{3}{5}$，求$\cos(2\alpha+\beta)$的值.

答案

2.

设函数$f(x)=\sin\omega x\cos\varphi+\cos\omega x\sin\varphi(\omega>0,|\varphi|<\dfrac{\pi}{2})$.

（1）若$f(0)=-\dfrac{\sqrt{3}}{2}$，求$\varphi$的值；

（2）已知$f(x)$在区间$[-\dfrac{\pi}{3},\dfrac{2\pi}{3}]$上单调递增，$f(\dfrac{2\pi}{3})=1$，再从条件①、条件②、条件③这三个条件中选择一个作为已知，使函数$f(x)$存在，求$\omega,\varphi$的值.

条件①：$f(\dfrac{\pi}{3})=\sqrt{2}$；

条件②：$f(-\dfrac{\pi}{3})=-1$；

条件③：$f(x)$在区间$[-\dfrac{\pi}{2},-\dfrac{\pi}{3}]$上单调递减.

注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合条件的条件分别解答，按第一个解答计分.

答案

3.

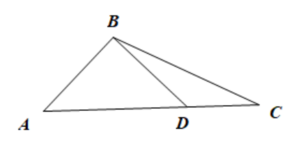
如图，在$\triangle ABC$中，点$D$在边$AC$上，且$AB\perp BD$. 已知$\cos A=2\sin\dfrac{A}{2}\sin\dfrac{\angle ABC+C}{2}$，$AB=\sqrt{2}$.

（1）求$A$；

（2）若$\triangle BCD$的面积为$\dfrac{1}{2}$，求$BC$.

答案