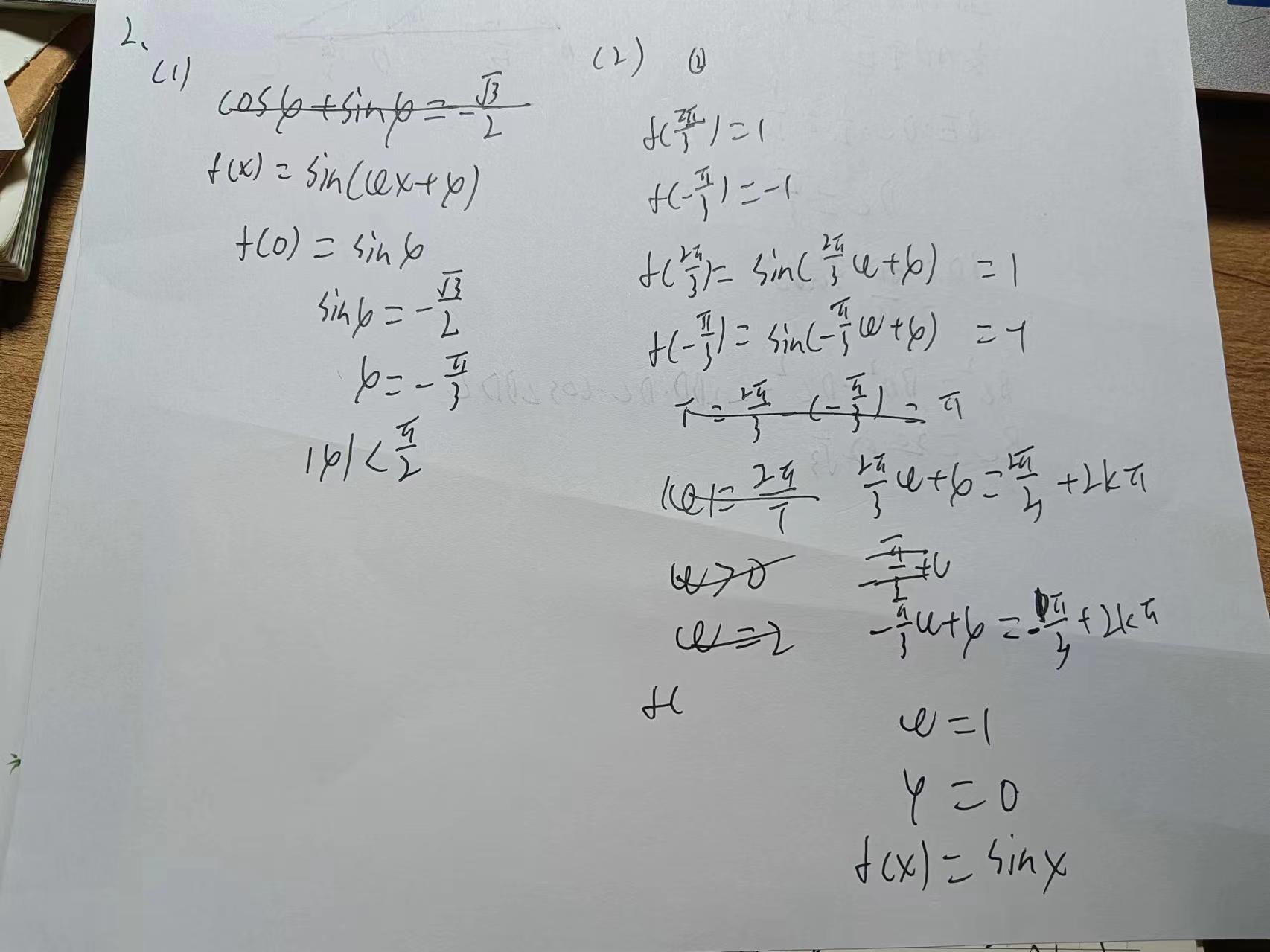讨论:必修一问题讨论:修订间差异
(→三角函数) |
(→2024/07/28 3: 回复) |
||
| (未显示3个用户的63个中间版本) | |||
| 第1行: | 第1行: | ||
== | == 一道三角函数题 == | ||
ω>0,0<φ<$\dfrac{π}{2}$,f(x)=$2sin$(ωx+φ)+3最小正周期为π,且图想过($\dfrac{π}{12}$,5) | ω>0,0<φ<$\dfrac{π}{2}$,f(x)=$2sin$(ωx+φ)+3最小正周期为π,且图想过($\dfrac{π}{12}$,5) | ||
| 第5行: | 第5行: | ||
(1)求f(x) | (1)求f(x) | ||
(2)当x∈[-$\dfrac{π}{6}$,$\dfrac{5π}{12}$],求f(x)的Max值,和min值. | |||
--[[用户:Cyx|Cyx]]([[用户讨论:Cyx|留言]]) 2024年3月3日 (日) 10:24 (CST) | |||
[[用户: | :输入得不规范,你比较一下我输的和你输入的源代码 | ||
:已知$\omega>0$,$0<\varphi<\dfrac{\pi}{2}$,函数$f(x)=2\sin(\omega x+\varphi)+3$的最小正周期为$\pi$,且其图像过$(\dfrac{\pi}{12},5)$ | |||
:(1) 求$f(x)$; | |||
:(2) 当$x∈[-\dfrac{\pi}{6},\dfrac{5\pi}{12}]$时,求$f(x)$的最大值和最小值. | |||
:--[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 11:02 (CST) | |||
:提示: | |||
:(1)周期为$\pi$,可以求出$\omega$,又过点$(\dfrac{\pi}{12},5)$,可求出$f(x)$ | |||
:(2)当$x\in[-\dfrac{\pi}{6},\dfrac{5\pi}{12}]$时,先求出$\omega x+\varphi$的范围,就可画出$f(x)$的图像了,从而可以求出最大最小值. | |||
:--[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 11:14 (CST) | |||
:再提示: | |||
:方程$\sin(\dfrac{\pi}{6}+\varphi)=1$我们解不了,但把$\dfrac{\pi}{6}+\varphi$当一整体,我们知道其范围,那么根据图象就可求出$\dfrac{\pi}{6}+\varphi$的值,从而求出$\varphi$的值。把$\dfrac{\pi}{6}+\varphi$当一整体,是本点的重点和难点。 | |||
:--[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 13:22 (CST) | |||
:[[/01|视频讲解]] | |||
:--[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 13:52 (CST) | |||
== 2024/5/25 == | |||
记函数f(x)=sin(ωx+$\dfrac{π}{4}$)(ω>0)的最小正周期为T,若$\dfrac{2π}{3}$<T<π,且y=f(x)的图像关于($\dfrac{3π}{2}$,0)中心对称,则f($\dfrac{π}{2}$)=() | |||
A.1 | |||
B.$\dfrac{5}{2}$ | |||
C.-1 | |||
D.3 | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年5月25日 (六) 23:01 (CST) | |||
:[[/02|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年6月2日 (日) 10:42 (CST) | |||
== 2024/6/01 == | |||
已知函数y=f(x)与y=g(x)有相同定义域D.若存在常数a(a$\in$R)使得对任意的$x_1$$\in$D,都存在$x_2$$\in$D,满足f($x_1$)+g($x_2$)=a,则称函数y=g(x)是函数y=f(x)关于a的“s函数” | |||
(1)若f(x)=$ln_x$,g(x)=$e^x$,试判断函数y=g(x)是否是y=f(x)关于0的“s函数”,并说明理由 | |||
(2)若函数y=f(x)与y=g(x)均存在最大值与最小值,且函数y=g(x)是y=f(x)关于a的“s函数”,y=f(x)又是y=g(x)关于a的的“s函数”,并证明: | |||
$[f(x)]_m$$_i$$_n$+$[g(x)]_m$$_a$$_x$=a | |||
(3)已知f(x)=|x–1|,g(x)=$\sqrt{x}$ | |||
,其定义域均为[0,t].若存在唯一的a,使得y=g(x)是y=(x)关于a的“s函数”,求t的所有可能值 | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年6月1日 (六) 22:10 (CST) | |||
== 2024/6/01 == | |||
(多选)已知f(0)=$\dfrac{1}{2}$,f(x+y)=f(x)f(1-y)+f(y)f(1-x),则() | |||
A.f(1)=$\dfrac{1}{2}$ | |||
B.f(x)=$\dfrac{1}{2}$恒成立 | |||
C.f(x+y)=2f(x)f(y) | |||
D.满足条件的f(x)不止一个 | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年6月1日 (六) 22:45 (CST) | |||
:[[/04|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年6月4日 (二) 19:23 (CST) | |||
== 2024/6/15 == | |||
已知函数f(x)的定义域为R,f(x)>f(x-1)+f(x-2),且当x<3时f(x)=x,则下列结论一定正确的是() | |||
A.f(10)>100 | |||
B.f(20)>1000 | |||
C.f(10)<1000 | |||
D.f(20)<10000 | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年6月15日 (六) 23:28 (CST) | |||
== 2024/6/15 == | |||
已知函数f(x)是一次函数,且满足f(x-1)+f(x)=2x-1 | |||
(1)求f(x)的解析式 | |||
(2)设g(1-$\dfrac{2}{x-1}$)f(x),x$\in$(-$\infty$,1) | |||
①是证明g(x)在(-$\infty$,1)上单调递增; | |||
②求g(x)在区间[0,3]上的最值 | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年6月15日 (六) 23:35 (CST) | |||
:[[/05|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年7月2日 (二) 11:07 (CST) | |||
== 2024/6/22 == | |||
已知f(x)是定义域在R上的偶函数,当∀$x_1$,$x_2$$\in$[0,$+\infty$],且$x_1$$\neq$$x_2$时,$\dfrac{f(1)f(2)}{x_1-x_2}$>4($x_1$+$x_2$)恒成立,f(2)=16,则满足f($ln^m$)$\leqslant$4f($ln^m$)的m取值范围为() | |||
已知$f(x)$是定义域在$R$上的偶函数,当$\forall x_1,x_2\in[0,+\infty)$,且$x_1\neq x_2$时,$\dfrac{f(x_1)-f(x_2)}{x_1-x_2}>4(x_1+x_2)$恒成立,$f(2)=16$,则满足$f(\ln m)\leqslant4(\ln m)^2$的$m$取值范围为() | |||
A.[$\dfrac{1}{e}$,e] | |||
B.[$\dfrac{1}{e^2}$,1] | |||
C.[1,$e^2$] | |||
D.[$\dfrac{1}{e^2}$,$e^2$] | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年6月22日 (六) 20:07 (CST) | |||
:[[/06|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年7月2日 (二) 11:08 (CST) | |||
== 2024/07/28 == | |||
[[文件:三角函数题一.jpg]] | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年7月28日 (日) 19:20 (CST) | |||
:[[/07|讲评]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年8月1日 (四) 12:45 (CST) | |||
== 2024/07/28 == | |||
[[文件:三角函数题二.jpg]] | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年7月28日 (日) 19:36 (CST) | |||
:[[/08|讲评]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年8月1日 (四) 12:45 (CST) | |||
== 2024/07/28 == | |||
[[文件:三角函数题三.jpg]] | |||
[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年7月28日 (日) 19:40 (CST) | |||
:[[/09|讲评]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年8月1日 (四) 12:46 (CST) | |||
2024年8月1日 (四) 12:46的最新版本
一道三角函数题
ω>0,0<φ<$\dfrac{π}{2}$,f(x)=$2sin$(ωx+φ)+3最小正周期为π,且图想过($\dfrac{π}{12}$,5)
(1)求f(x)
(2)当x∈[-$\dfrac{π}{6}$,$\dfrac{5π}{12}$],求f(x)的Max值,和min值.
--Cyx(留言) 2024年3月3日 (日) 10:24 (CST)
- 输入得不规范,你比较一下我输的和你输入的源代码
- 已知$\omega>0$,$0<\varphi<\dfrac{\pi}{2}$,函数$f(x)=2\sin(\omega x+\varphi)+3$的最小正周期为$\pi$,且其图像过$(\dfrac{\pi}{12},5)$
- (1) 求$f(x)$;
- (2) 当$x∈[-\dfrac{\pi}{6},\dfrac{5\pi}{12}]$时,求$f(x)$的最大值和最小值.
- --Admin(留言) 2024年3月3日 (日) 11:02 (CST)
- 提示:
- (1)周期为$\pi$,可以求出$\omega$,又过点$(\dfrac{\pi}{12},5)$,可求出$f(x)$
- (2)当$x\in[-\dfrac{\pi}{6},\dfrac{5\pi}{12}]$时,先求出$\omega x+\varphi$的范围,就可画出$f(x)$的图像了,从而可以求出最大最小值.
- --Admin(留言) 2024年3月3日 (日) 11:14 (CST)
- 再提示:
- 方程$\sin(\dfrac{\pi}{6}+\varphi)=1$我们解不了,但把$\dfrac{\pi}{6}+\varphi$当一整体,我们知道其范围,那么根据图象就可求出$\dfrac{\pi}{6}+\varphi$的值,从而求出$\varphi$的值。把$\dfrac{\pi}{6}+\varphi$当一整体,是本点的重点和难点。
- --Admin(留言) 2024年3月3日 (日) 13:22 (CST)
- 视频讲解
- --Admin(留言) 2024年3月3日 (日) 13:52 (CST)
2024/5/25
记函数f(x)=sin(ωx+$\dfrac{π}{4}$)(ω>0)的最小正周期为T,若$\dfrac{2π}{3}$<T<π,且y=f(x)的图像关于($\dfrac{3π}{2}$,0)中心对称,则f($\dfrac{π}{2}$)=()
A.1
B.$\dfrac{5}{2}$
C.-1
D.3
Cyc(留言) 2024年5月25日 (六) 23:01 (CST)
2024/6/01
已知函数y=f(x)与y=g(x)有相同定义域D.若存在常数a(a$\in$R)使得对任意的$x_1$$\in$D,都存在$x_2$$\in$D,满足f($x_1$)+g($x_2$)=a,则称函数y=g(x)是函数y=f(x)关于a的“s函数”
(1)若f(x)=$ln_x$,g(x)=$e^x$,试判断函数y=g(x)是否是y=f(x)关于0的“s函数”,并说明理由
(2)若函数y=f(x)与y=g(x)均存在最大值与最小值,且函数y=g(x)是y=f(x)关于a的“s函数”,y=f(x)又是y=g(x)关于a的的“s函数”,并证明: $[f(x)]_m$$_i$$_n$+$[g(x)]_m$$_a$$_x$=a
(3)已知f(x)=|x–1|,g(x)=$\sqrt{x}$
,其定义域均为[0,t].若存在唯一的a,使得y=g(x)是y=(x)关于a的“s函数”,求t的所有可能值
Cyc(留言) 2024年6月1日 (六) 22:10 (CST)
2024/6/01
(多选)已知f(0)=$\dfrac{1}{2}$,f(x+y)=f(x)f(1-y)+f(y)f(1-x),则()
A.f(1)=$\dfrac{1}{2}$
B.f(x)=$\dfrac{1}{2}$恒成立
C.f(x+y)=2f(x)f(y)
D.满足条件的f(x)不止一个
Cyc(留言) 2024年6月1日 (六) 22:45 (CST)
2024/6/15
已知函数f(x)的定义域为R,f(x)>f(x-1)+f(x-2),且当x<3时f(x)=x,则下列结论一定正确的是()
A.f(10)>100
B.f(20)>1000
C.f(10)<1000
D.f(20)<10000
Cyc(留言) 2024年6月15日 (六) 23:28 (CST)
2024/6/15
已知函数f(x)是一次函数,且满足f(x-1)+f(x)=2x-1
(1)求f(x)的解析式
(2)设g(1-$\dfrac{2}{x-1}$)f(x),x$\in$(-$\infty$,1)
①是证明g(x)在(-$\infty$,1)上单调递增; ②求g(x)在区间[0,3]上的最值
Cyc(留言) 2024年6月15日 (六) 23:35 (CST)
2024/6/22
已知f(x)是定义域在R上的偶函数,当∀$x_1$,$x_2$$\in$[0,$+\infty$],且$x_1$$\neq$$x_2$时,$\dfrac{f(1)f(2)}{x_1-x_2}$>4($x_1$+$x_2$)恒成立,f(2)=16,则满足f($ln^m$)$\leqslant$4f($ln^m$)的m取值范围为()
已知$f(x)$是定义域在$R$上的偶函数,当$\forall x_1,x_2\in[0,+\infty)$,且$x_1\neq x_2$时,$\dfrac{f(x_1)-f(x_2)}{x_1-x_2}>4(x_1+x_2)$恒成立,$f(2)=16$,则满足$f(\ln m)\leqslant4(\ln m)^2$的$m$取值范围为()
A.[$\dfrac{1}{e}$,e]
B.[$\dfrac{1}{e^2}$,1]
C.[1,$e^2$]
D.[$\dfrac{1}{e^2}$,$e^2$]
Cyc(留言) 2024年6月22日 (六) 20:07 (CST)
2024/07/28
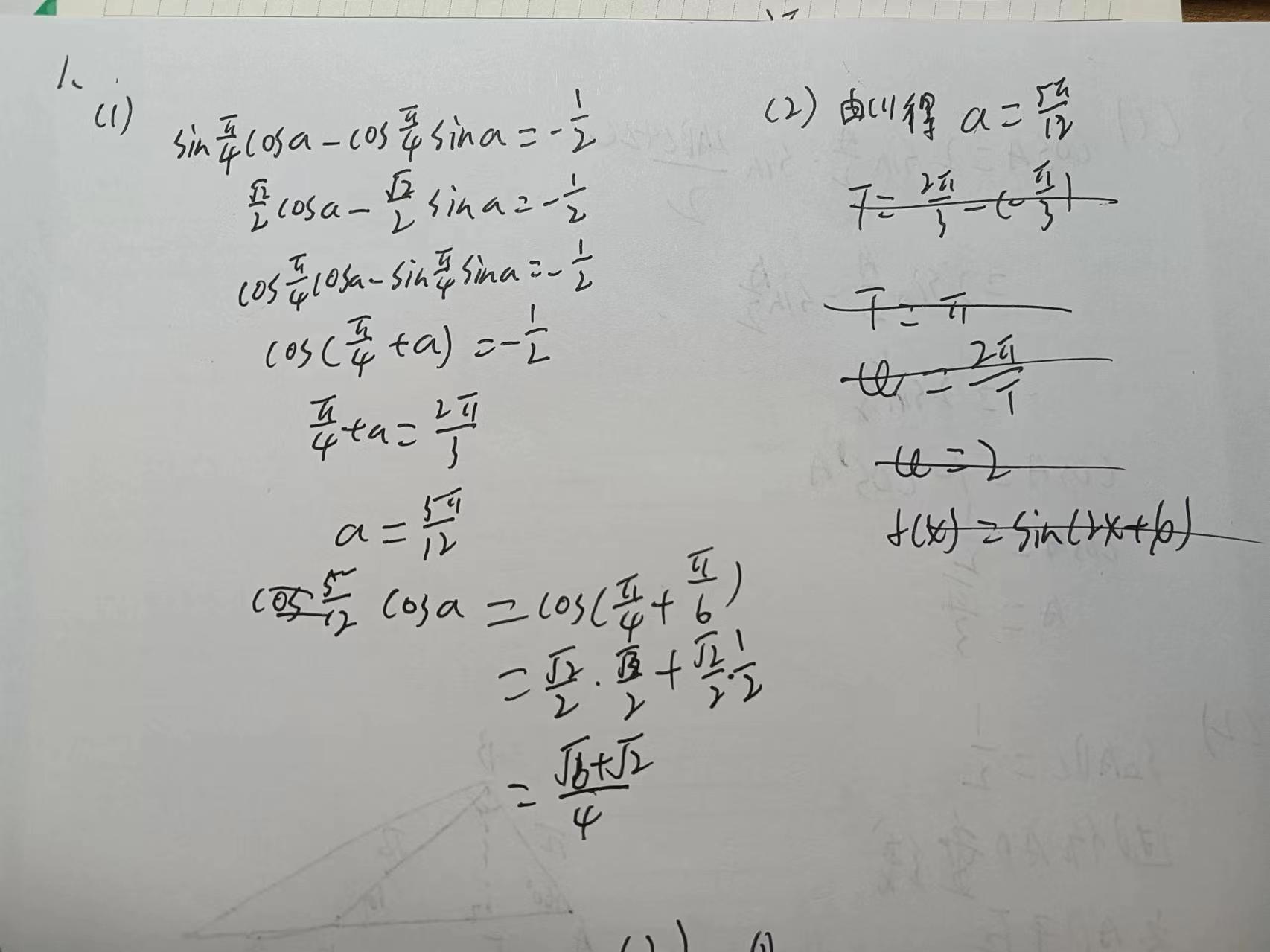 Cyc(留言) 2024年7月28日 (日) 19:20 (CST)
Cyc(留言) 2024年7月28日 (日) 19:20 (CST)
2024/07/28
Cyc(留言) 2024年7月28日 (日) 19:36 (CST)