讨论:平面向量及其应用复习:修订间差异
无编辑摘要 |
(→2024/4/27: 回复) |
||
| (未显示2个用户的64个中间版本) | |||
| 第7行: | 第7行: | ||
--[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 08:52 (CST) | --[[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月3日 (日) 08:52 (CST) | ||
:现在开始回复,回复完了,记得换行,并输入两个减号--,两减号的意思是上面的话是谁说的。 | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月10日 (日) 10:58 (CST) | |||
== 2024/03/10 == | |||
[[文件:Cyc10.jpg|right|缩略图]] | |||
如图在所示平面直角坐标系中,已知点A(1,0)和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ,其中O为坐标原点 | |||
= | (1)若θ=$\dfrac{3π}{4}$设点D为线段OA上的动点,求|$\overrightarrow{OC}$+$\overrightarrow{OD}$|的最小值 | ||
(2)θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值 | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年3月10日 (日) 10:36 (CST) | |||
:在第(1)问中,点$C$的坐标为$(\cos\dfrac{3\pi}{4},\sin\dfrac{3\pi}{4})$,在第(2)问中,点$C$的坐标为$(\cos\theta,\sin\theta)$,理由是三角函数的定义$\sin\theta=\dfrac{y}{r}$,$\cos\theta=\dfrac{x}{r}$,本题中$\angle AOC$的始边与$x$轴的正半轴重合,点$C$是其终边上的一点,符合三角函数的定义所需的环境,点$C(x,y)$,$r=|\overrightarrow{OC}|=1$ | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月10日 (日) 13:43 (CST) | |||
:输入还可以更好一点,比如只要是非中文的内容都应用美元号夹起来,题号可以不夹,不夹起来和夹起来的字体是不一样的,数学中是没有中文的句号,只能用英文的点号加上空格,但逗号中英文都有,但英文的逗号间距太小,所有要转换到中文状态下输。即逗号要用中文的,句号要用英文的。 | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月10日 (日) 13:53 (CST) | |||
:$\vec{n}=(1-\cos\theta,\sin\theta-2\cos\theta)$,我按这个讲 | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月10日 (日) 14:12 (CST) | |||
:[[/01|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月10日 (日) 15:44 (CST) | |||
== 2024/3/15 == | |||
如图,在正方形ABCD中,AB=2,E为BC中点,P是以AB为直径的圆弧上任意一点,则 | |||
$\overrightarrow{AE}$·$\overrightarrow{AP}$的最大值() | |||
[[文件:Cyc11.jpg|缩略图]] | |||
A.4 | |||
B.5 | |||
C.$\sqrt{5}$ | |||
D.2+$\sqrt{5}$ | |||
填空题:向量a=(2,1)在向量b=(3,4)方向上的投影向量的坐标为( ) | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年3月15日 (五) 20:55 (CST) | |||
:[[/02|第1小题视频讲解]] | |||
:[[/03|第2小题视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年3月21日 (四) 10:10 (CST) | |||
== 2024/3/22 == | |||
在△ABC中,AB=2,AC=1,$\angle$ACB=$\dfrac{π}{2}$,D是线段BC上的一点,且$\overrightarrow{BD}$=$\dfrac{1}{2}$$\overrightarrow{DC}$,F为线段AB上一点 | |||
(1)若$\overrightarrow{AD}=x\overrightarrow{AB}+y\overrightarrow{AC}$,求实数$x-y$的值; | |||
(2)求$\overrightarrow{CF}$·$\overrightarrow{FA}$的 | |||
取值范围 | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年3月22日 (五) 22:37 (CST) | |||
:[[/04|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月4日 (四) 21:52 (CST) | |||
== 2024/3/24 == | |||
(多选)以知锐角△ABC三个内角A,B,C的对应边分别为a,b,c,且 $\angle $C=$\dfrac{π}{3}$,c=2.则下列结论正确的是() | |||
A.△ABC面积最大为2 | |||
B.$\overrightarrow{AC}$·$\overrightarrow{AB}$的取值范围为(0,4) | |||
C.bcosA+acosB=2 | |||
D.$\dfrac{cosB}{cosA}$的取值范围是(0,+∞) | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年3月24日 (日) 13:17 (CST) | |||
:[[/06|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月5日 (五) 09:25 (CST) | |||
== 2024/4/2 == | |||
△ABC,已知($\dfrac{\overrightarrow{AB}}{|AB|}$+$\dfrac{\overrightarrow{AC}}{|AC|}$ | |||
)·$\overrightarrow{BC}$=0,$\dfrac{\overrightarrow{AB}}{|AB|}$•$\dfrac{\overrightarrow{BC}}{|BC|}$ | |||
=-$\dfrac{\sqrt{2}}{2}$,则△ABC为() | |||
A.三边互不相等的三角形 | |||
B.等边三角形 | |||
C.等腰直角三角形 | |||
D.顶角为钝角的等腰三角形 | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年4月2日 (二) 11:39 (CST) | |||
:[[/05|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月4日 (四) 22:01 (CST) | |||
== 2024/4/3 == | |||
(多选)设向量$\overrightarrow{a}$=(k,2),$\overrightarrow{b}$=(1,-1),则下列叙述错误的是() | |||
A.若k<-2时,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角 | |||
B.|$\overrightarrow{a}$|的最小值为2 | |||
C.与$\overrightarrow{b}$共线的单位向量只有一个为($\dfrac{\sqrt{2}}{2}$,-$\dfrac{\sqrt{2}}{2}$) | |||
D.若|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|则k=$\dfrac{\sqrt{2}}{2}$或-$\dfrac{\sqrt{2}}{2}$ | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年4月3日 (三) 22:08 (CST) | |||
:[[/07|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月21日 (日) 10:24 (CST) | |||
== 2024/4/20 == | |||
(多选)已知$\overrightarrow{OP}$=($\dfrac{\sqrt{5}}{5}$,$\dfrac{2\sqrt{5}}{5}$),将$\overrightarrow{OP}$绕坐标原点分别旋转-30°,30°,60°到,$\overrightarrow{OP}_1$, | |||
$\overrightarrow{OP}_2$,$\overrightarrow{OP}_3$的位置,则() | |||
A.$\overrightarrow{OP}_1$•$\overrightarrow{OP}_2$=$\dfrac{\sqrt{3}}{2}$ | |||
B.$|\overrightarrow{PP}_1|$=$|\overrightarrow{P_1P_2}|$ | |||
C.$\overrightarrow{OP}$•$\overrightarrow{OP}_3$=$\overrightarrow{OP}_1$•$\overrightarrow{OP}_2$ | |||
D.点$P_1$坐标为($\dfrac{\sqrt{15}+2\sqrt{5}}{10}$,$\dfrac{2\sqrt{15}-\sqrt{5}}{10}$) | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年4月20日 (六) 20:41 (CST) | |||
:[[/08|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月21日 (日) 10:22 (CST) | |||
== 2024/4/27 == | |||
如图,平行四边形ABCD中,M是BC中点,N是CD上靠近靠近点D的三等分点,若 $\overrightarrow{AB}$\=λ$\overrightarrow{AM}$+μ$\overrightarrow{AN}$则λ+μ=() | |||
[[文件:Cyc14.jpg|right|缩略图]] | |||
A.-$\dfrac{9}{5}$ | |||
B.-$\dfrac{3}{5}$ | |||
C.$\dfrac{9}{5}$ | |||
D.$\dfrac{3}{5}$ | |||
备注:用常规方法做一遍后发现做部出来,于是就想到要用辅助线,但是不知道咋做辅助线 | |||
--[[用户:Cyc|Cyc]]([[用户讨论:Cyc|留言]]) 2024年4月27日 (六) 19:53 (CST) | |||
:[[/09|视频讲解]] | |||
:-- [[用户:Admin|Admin]]([[用户讨论:Admin|留言]]) 2024年4月28日 (日) 21:15 (CST) | |||
2024年4月28日 (日) 21:15的最新版本
我有一个问题
这里是问题的描述。
--Admin(留言) 2024年3月3日 (日) 08:52 (CST)
- 现在开始回复,回复完了,记得换行,并输入两个减号--,两减号的意思是上面的话是谁说的。
- -- Admin(留言) 2024年3月10日 (日) 10:58 (CST)
2024/03/10
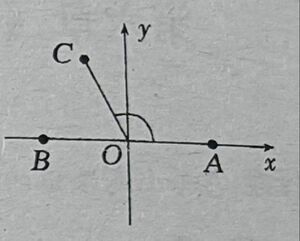
如图在所示平面直角坐标系中,已知点A(1,0)和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ,其中O为坐标原点
(1)若θ=$\dfrac{3π}{4}$设点D为线段OA上的动点,求|$\overrightarrow{OC}$+$\overrightarrow{OD}$|的最小值
(2)θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值
--Cyc(留言) 2024年3月10日 (日) 10:36 (CST)
- 在第(1)问中,点$C$的坐标为$(\cos\dfrac{3\pi}{4},\sin\dfrac{3\pi}{4})$,在第(2)问中,点$C$的坐标为$(\cos\theta,\sin\theta)$,理由是三角函数的定义$\sin\theta=\dfrac{y}{r}$,$\cos\theta=\dfrac{x}{r}$,本题中$\angle AOC$的始边与$x$轴的正半轴重合,点$C$是其终边上的一点,符合三角函数的定义所需的环境,点$C(x,y)$,$r=|\overrightarrow{OC}|=1$
- -- Admin(留言) 2024年3月10日 (日) 13:43 (CST)
- 输入还可以更好一点,比如只要是非中文的内容都应用美元号夹起来,题号可以不夹,不夹起来和夹起来的字体是不一样的,数学中是没有中文的句号,只能用英文的点号加上空格,但逗号中英文都有,但英文的逗号间距太小,所有要转换到中文状态下输。即逗号要用中文的,句号要用英文的。
- -- Admin(留言) 2024年3月10日 (日) 13:53 (CST)
- $\vec{n}=(1-\cos\theta,\sin\theta-2\cos\theta)$,我按这个讲
- -- Admin(留言) 2024年3月10日 (日) 14:12 (CST)
- 视频讲解
- -- Admin(留言) 2024年3月10日 (日) 15:44 (CST)
2024/3/15
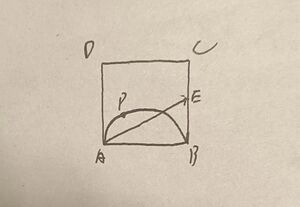
如图,在正方形ABCD中,AB=2,E为BC中点,P是以AB为直径的圆弧上任意一点,则 $\overrightarrow{AE}$·$\overrightarrow{AP}$的最大值()
A.4
B.5
C.$\sqrt{5}$
D.2+$\sqrt{5}$
填空题:向量a=(2,1)在向量b=(3,4)方向上的投影向量的坐标为( )
--Cyc(留言) 2024年3月15日 (五) 20:55 (CST)
2024/3/22
在△ABC中,AB=2,AC=1,$\angle$ACB=$\dfrac{π}{2}$,D是线段BC上的一点,且$\overrightarrow{BD}$=$\dfrac{1}{2}$$\overrightarrow{DC}$,F为线段AB上一点
(1)若$\overrightarrow{AD}=x\overrightarrow{AB}+y\overrightarrow{AC}$,求实数$x-y$的值;
(2)求$\overrightarrow{CF}$·$\overrightarrow{FA}$的 取值范围
--Cyc(留言) 2024年3月22日 (五) 22:37 (CST)
2024/3/24
(多选)以知锐角△ABC三个内角A,B,C的对应边分别为a,b,c,且 $\angle $C=$\dfrac{π}{3}$,c=2.则下列结论正确的是()
A.△ABC面积最大为2
B.$\overrightarrow{AC}$·$\overrightarrow{AB}$的取值范围为(0,4)
C.bcosA+acosB=2
D.$\dfrac{cosB}{cosA}$的取值范围是(0,+∞)
--Cyc(留言) 2024年3月24日 (日) 13:17 (CST)
2024/4/2
△ABC,已知($\dfrac{\overrightarrow{AB}}{|AB|}$+$\dfrac{\overrightarrow{AC}}{|AC|}$ )·$\overrightarrow{BC}$=0,$\dfrac{\overrightarrow{AB}}{|AB|}$•$\dfrac{\overrightarrow{BC}}{|BC|}$ =-$\dfrac{\sqrt{2}}{2}$,则△ABC为()
A.三边互不相等的三角形
B.等边三角形
C.等腰直角三角形
D.顶角为钝角的等腰三角形
--Cyc(留言) 2024年4月2日 (二) 11:39 (CST)
2024/4/3
(多选)设向量$\overrightarrow{a}$=(k,2),$\overrightarrow{b}$=(1,-1),则下列叙述错误的是()
A.若k<-2时,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角
B.|$\overrightarrow{a}$|的最小值为2
C.与$\overrightarrow{b}$共线的单位向量只有一个为($\dfrac{\sqrt{2}}{2}$,-$\dfrac{\sqrt{2}}{2}$)
D.若|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|则k=$\dfrac{\sqrt{2}}{2}$或-$\dfrac{\sqrt{2}}{2}$
--Cyc(留言) 2024年4月3日 (三) 22:08 (CST)
2024/4/20
(多选)已知$\overrightarrow{OP}$=($\dfrac{\sqrt{5}}{5}$,$\dfrac{2\sqrt{5}}{5}$),将$\overrightarrow{OP}$绕坐标原点分别旋转-30°,30°,60°到,$\overrightarrow{OP}_1$, $\overrightarrow{OP}_2$,$\overrightarrow{OP}_3$的位置,则()
A.$\overrightarrow{OP}_1$•$\overrightarrow{OP}_2$=$\dfrac{\sqrt{3}}{2}$
B.$|\overrightarrow{PP}_1|$=$|\overrightarrow{P_1P_2}|$
C.$\overrightarrow{OP}$•$\overrightarrow{OP}_3$=$\overrightarrow{OP}_1$•$\overrightarrow{OP}_2$
D.点$P_1$坐标为($\dfrac{\sqrt{15}+2\sqrt{5}}{10}$,$\dfrac{2\sqrt{15}-\sqrt{5}}{10}$)
--Cyc(留言) 2024年4月20日 (六) 20:41 (CST)
2024/4/27
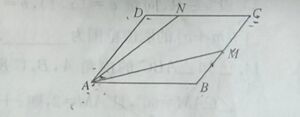
如图,平行四边形ABCD中,M是BC中点,N是CD上靠近靠近点D的三等分点,若 $\overrightarrow{AB}$\=λ$\overrightarrow{AM}$+μ$\overrightarrow{AN}$则λ+μ=()
A.-$\dfrac{9}{5}$
B.-$\dfrac{3}{5}$
C.$\dfrac{9}{5}$
D.$\dfrac{3}{5}$
备注:用常规方法做一遍后发现做部出来,于是就想到要用辅助线,但是不知道咋做辅助线