1102 空间向量的应用:修订间差异
| (未显示同一用户的32个中间版本) | |||
| 第1行: | 第1行: | ||
==知识要点== | ==知识要点== | ||
[[/1102|视频讲解]] | |||
==例题== | ==例题== | ||
===1、2021全国甲理,19=== | |||
[[文件:2024061907.png|缩略图|右]] | |||
如图,已知直三棱柱$ABC-A_1B_1C_1$中,侧面$AA_1B_1B$为正方形,$AB=BC=2$,$E,F$分别为$AC$和$CC_1$的中点,$D$为棱$A_1B_1$上的点,$BF\perp A_1B_1$. | |||
(1)证明:$BF\perp DE$; | |||
(2)当$B_1D$为何值时,面$BB_1C_1C$与面$DFE$所成的二面角的正弦值最小? | |||
[[/000101|答案]] [[/000102|视频讲解]] | |||
===4、2022全国乙理,18=== | |||
[[文件:2024061908.png|缩略图|右]] | |||
如图,四面体$ABCD$中,$AD\perp CD$,$AD=CD$,$\angle ADB=\angle BDC$,$E$为$AC$的中点. | |||
(1)求证:平面$BED\perp$平面$ACD$; | |||
(2)设$AB=BD=2$,$\angle ACB=60^\circ$,点$F$在$BD$上,当$\triangle AFC$的面积最小时,求$CF$与平面$ABD$所成的角的正弦值. | |||
| 第21行: | 第32行: | ||
[[/000201|答案]] [[/000202|视频讲解]] | |||
==练习== | ==练习== | ||
| 第47行: | 第54行: | ||
D. 直线$BC_1$与平面$ABCD$所成的角为$45^\circ$ | D. 直线$BC_1$与平面$ABCD$所成的角为$45^\circ$ | ||
===3、2023新高考Ⅰ,18=== | |||
[[文件:2024061904.png|缩略图|右]] | |||
如图,在正四棱柱$ABCD-A_1B_1C_1D_1$中,$AB=2$,$AA_1=4$,点$A_2,B_2,C_2,D_2$分别在棱$AA_1,BB_1,CC_1,DD_1$上,$AA_2=1,BB_2=DD_2=2,CC_2=3$. | |||
(1)证明:$B_2C_2\parallel A_2D_2$; | |||
(2)点$P$在棱$BB_1$上,当二面角$P-A_2C_2-D_2$为$150^\circ$时,求$B_2P$. | |||
[[/010301|答案]] | |||
===4、2023新课标Ⅱ,20=== | |||
[[文件:2024061905.png|缩略图|右]] | |||
如图,三棱锥$A-BCD$中,$DA=DB=DC$,$BD\perp CD$,$\angle ADB=\angle ADC=60^\circ$,$E$为$BC$的中点. | |||
(1)证明:$BC\perp DA$; | |||
(2)点$F$满足$\overrightarrow{EF}=\overrightarrow{DA}$,求二面角$D-AB-F$的正弦值. | |||
[[/010401|答案]] | |||
[[category:立体几何]] | [[category:立体几何]] | ||
2024年7月22日 (一) 10:27的最新版本
知识要点
例题
1、2021全国甲理,19
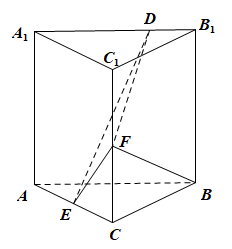
如图,已知直三棱柱$ABC-A_1B_1C_1$中,侧面$AA_1B_1B$为正方形,$AB=BC=2$,$E,F$分别为$AC$和$CC_1$的中点,$D$为棱$A_1B_1$上的点,$BF\perp A_1B_1$.
(1)证明:$BF\perp DE$;
(2)当$B_1D$为何值时,面$BB_1C_1C$与面$DFE$所成的二面角的正弦值最小?
4、2022全国乙理,18
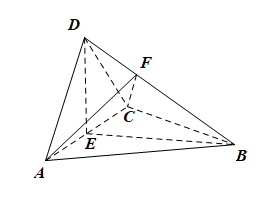
如图,四面体$ABCD$中,$AD\perp CD$,$AD=CD$,$\angle ADB=\angle BDC$,$E$为$AC$的中点.
(1)求证:平面$BED\perp$平面$ACD$;
(2)设$AB=BD=2$,$\angle ACB=60^\circ$,点$F$在$BD$上,当$\triangle AFC$的面积最小时,求$CF$与平面$ABD$所成的角的正弦值.
练习
1、2023全国乙理,9
已知$\triangle ABC$为等腰直角三角形,$AB$为斜边,$\triangle ABD$为等边三角形. 若二面角$C-AB-D$为$150^\circ$,则直线$CD$与平面$ABC$所成角的正切值为$(\qquad)$.
A. $\dfrac{1}{5}\qquad$B. $\dfrac{\sqrt{2}}{5}\qquad$C.$\dfrac{\sqrt{3}}{5}\qquad$D. $\dfrac{2}{5}\qquad$
2、2022新高考Ⅰ,9
(多选)已知正方体$ABCD-A_1B_1C_1D_1$,则$(\qquad)$
A. 直线$BC_1$与$DA_1$所成的角为$90^\circ$
B. 直线$BC_1$与$CA_1$所成的角为$90^\circ$
C. 直线$BC_1$与平面$BB_1D_1D$所成的角为$45^\circ$
D. 直线$BC_1$与平面$ABCD$所成的角为$45^\circ$
3、2023新高考Ⅰ,18
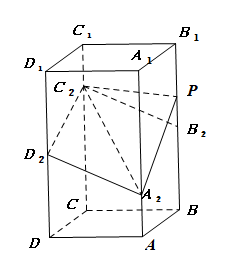
如图,在正四棱柱$ABCD-A_1B_1C_1D_1$中,$AB=2$,$AA_1=4$,点$A_2,B_2,C_2,D_2$分别在棱$AA_1,BB_1,CC_1,DD_1$上,$AA_2=1,BB_2=DD_2=2,CC_2=3$.
(1)证明:$B_2C_2\parallel A_2D_2$;
(2)点$P$在棱$BB_1$上,当二面角$P-A_2C_2-D_2$为$150^\circ$时,求$B_2P$.
4、2023新课标Ⅱ,20
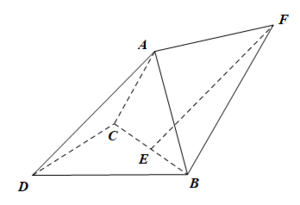
如图,三棱锥$A-BCD$中,$DA=DB=DC$,$BD\perp CD$,$\angle ADB=\angle ADC=60^\circ$,$E$为$BC$的中点.
(1)证明:$BC\perp DA$;
(2)点$F$满足$\overrightarrow{EF}=\overrightarrow{DA}$,求二面角$D-AB-F$的正弦值.