3.4 函数的应用(一):修订间差异
来自高中数学
无编辑摘要 |
(→例2) |
||
| (未显示同一用户的10个中间版本) | |||
| 第1行: | 第1行: | ||
==例题== | ==例题== | ||
===例1=== | |||
设小王的专项扣除比例、专项附加扣除金额、依法确定的其它扣除金额与3.1.2例8相同,全年综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税? | |||
[[/01340001|视频讲解]] | |||
===例2=== | |||
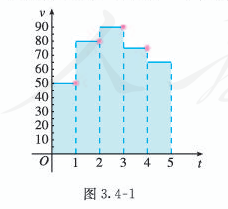
一辆汽车在某段路程中行驶的平均速率$v$(单位:km/h)与时间$t$(单位:h)的关系如图3.4-1所示, | |||
[[文件:01340002.png]] | |||
(1)求图3.4-1中阴影部分的面积,并说明所求面积的实际含义; | |||
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数是2004 km,试建立行驶这段路程时汽车里程表读数$s$(单位:km)与时间$t$的函数表达式,并画出相应的图象. | |||
[[/01340002|视频讲解]] [[/013400021|答案]] | |||
==练习== | ==练习== | ||
==习题3.4== | ==习题3.4== | ||
[[category:第三章 | [[category:第三章 函数的概念与性质]] | ||