7.1.1 条件概率:修订间差异
无编辑摘要 |
(→练习) |
||
| (未显示同一用户的10个中间版本) | |||
| 第1行: | 第1行: | ||
[[7.1 条件概率与全概率公式]] | |||
==知识要点== | ==知识要点== | ||
* 条件概率 | * 条件概率 | ||
| 第4行: | 第5行: | ||
* 概率的乘法公式 | * 概率的乘法公式 | ||
由条件概率的定义,对任意两个事件$A$与$B$,若$P(A)>0$,则$$P(AB)=P(A)P(B|A)$$ | 由条件概率的定义,对任意两个事件$A$与$B$,若$P(A)>0$,则$$P(AB)=P(A)P(B|A)$$ | ||
我们称上式为概率的乘法公式. | |||
==导入== | |||
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示. | |||
[[文件:2024040701.png]] | |||
在班级里随机选择一人做代表. | |||
(1)选到男生的概率是多少? | |||
(2)如果已知选到的是团员,那么选到的是男生的概率是多少? | |||
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭. 随机选择一个家庭,那么 | |||
(1)该家庭中两个小孩都是女孩的概率是多大? | |||
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大? | |||
==例题== | |||
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽取1道题,抽出的题不再放回. 求: | |||
(1)第1次抽到代数题且第2次抽到几何题的概率; | |||
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率. | |||
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗? | |||
例3 银行储蓄卡的密码由6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求: | |||
(1)任意按最后1位数字,不超过2次就按对的概率; | |||
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率. | |||
==练习== | |||
1.设$A\subseteq B$,且$P(A)=0.3$,$P(B)=0.6$. 根据事件包含关系的意义及条件概率的意义,直接写出$P(B|A)$和$P(A|B)$的值,再由条件概率公式进行验证. | |||
[[/01|答案]] | |||
2.从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回. 已知第1次抽到A牌,求第2次抽到A牌的概率. | |||
[[/02|答案]] | |||
3.袋子中有10个大小相同的球,其中7个白球,3个黑球. 每次从袋子中随机摸出1个球,摸出的球不再放回,求: | |||
(1)在第1次摸到白球的条件下,第2次摸到白球的概率; | |||
(2)两次都摸到白球的概率. | |||
[[/03|答案]] | |||
2024年4月8日 (一) 08:39的最新版本
知识要点
- 条件概率
一般地,设$A$,$B$为两个随机事件,且$P(A)>0$,我们称$$P(B|A)=\dfrac{P(AB)}{P(A)}$$为事件$A$发生的条件下,事件$B$发生的条件概率,简称条件概率.
- 概率的乘法公式
由条件概率的定义,对任意两个事件$A$与$B$,若$P(A)>0$,则$$P(AB)=P(A)P(B|A)$$ 我们称上式为概率的乘法公式.
导入
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示.
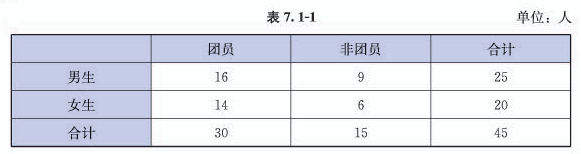
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭. 随机选择一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
例题
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽取1道题,抽出的题不再放回. 求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗?
例3 银行储蓄卡的密码由6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
练习
1.设$A\subseteq B$,且$P(A)=0.3$,$P(B)=0.6$. 根据事件包含关系的意义及条件概率的意义,直接写出$P(B|A)$和$P(A|B)$的值,再由条件概率公式进行验证.
2.从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回. 已知第1次抽到A牌,求第2次抽到A牌的概率.
3.袋子中有10个大小相同的球,其中7个白球,3个黑球. 每次从袋子中随机摸出1个球,摸出的球不再放回,求:
(1)在第1次摸到白球的条件下,第2次摸到白球的概率;
(2)两次都摸到白球的概率.