讨论:8.1 基本立体图形：修订间差异
来自高中数学
最新留言：2024年6月2日 (星期日)由Admin在话题2024/5/25内发布
（→2024/5/25： 回复） |
|||
| （未显示同一用户的2个中间版本） | |||
| 第1行： | 第1行： | ||
== 2024/5/25 == | == 2024/5/25 == | ||
[[文件:Cyc17.jpg|缩略图]] | |||
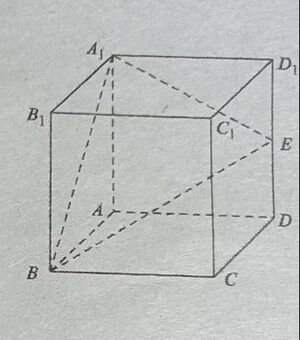
（多选）正方体ABCD-$A_1$$B_1$$C_1$$D_1$的棱长为2， | （多选）正方体ABCD-$A_1$$B_1$$C_1$$D_1$的棱长为2， | ||
E是棱D$D_1$的中点，F是侧面CD$C_1$$D_1$上的动点，且满足$B_1$F∥平面$A_1$BE，则下列结论正确的是（） | E是棱D$D_1$的中点，F是侧面CD$C_1$$D_1$上的动点，且满足$B_1$F∥平面$A_1$BE，则下列结论正确的是（） | ||
| 第13行： | 第14行： | ||
CD$D_1$$C_1$所成二面角的正弦值为$\dfrac{1}{3}$ | CD$D_1$$C_1$所成二面角的正弦值为$\dfrac{1}{3}$ | ||
[[用户:Cyc|Cyc]]（[[用户讨论:Cyc|留言]]） 2024年5月25日 (六) 22:34 (CST) | |||
[[ | :[[/01|视频讲解]] | ||
:-- [[用户:Admin|Admin]]（[[用户讨论:Admin|留言]]） 2024年6月2日 (日) 12:46 (CST) | |||
[[用户: | |||
2024年6月2日 (日) 12:46的最新版本
2024/5/25
（多选）正方体ABCD-$A_1$$B_1$$C_1$$D_1$的棱长为2， E是棱D$D_1$的中点，F是侧面CD$C_1$$D_1$上的动点，且满足$B_1$F∥平面$A_1$BE，则下列结论正确的是（）
A.平面$A_1$BE截正方体ABCD-$A_1$$B_1$$C_1$$D_1$所的截面面积为$\dfrac{9}{2}$
B.点F的轨迹长度为$\dfrac{π}{4}$
C.存在点F，使得$B_1$F$\perp$C$D_1$
D.平面$A_1$BE与平面 CD$D_1$$C_1$所成二面角的正弦值为$\dfrac{1}{3}$
