讨论:平面向量及其应用复习

我有一个问题

这里是问题的描述。

--Admin（留言） 2024年3月3日 (日) 08:52 (CST)

现在开始回复，回复完了，记得换行，并输入两个减号--，两减号的意思是上面的话是谁说的。

-- Admin（留言） 2024年3月10日 (日) 10:58 (CST)

2024/03/10

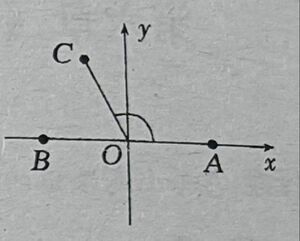
如图在所示平面直角坐标系中,已知点A（1,0）和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ，其中O为坐标原点

（1）若θ=$\dfrac{3π}{4}$设点D为线段OA上的动点，求|$\overrightarrow{OC}$+$\overrightarrow{OD}$|的最小值

（2）θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值

--Cyc（留言） 2024年3月10日 (日) 10:36 (CST)

在第（1）问中，点$C$的坐标为$(\cos\dfrac{3\pi}{4},\sin\dfrac{3\pi}{4})$，在第（2）问中，点$C$的坐标为$(\cos\theta,\sin\theta)$，理由是三角函数的定义$\sin\theta=\dfrac{y}{r}$，$\cos\theta=\dfrac{x}{r}$，本题中$\angle AOC$的始边与$x$轴的正半轴重合，点$C$是其终边上的一点，符合三角函数的定义所需的环境，点$C(x,y)$，$r=|\overrightarrow{OC}|=1$

-- Admin（留言） 2024年3月10日 (日) 13:43 (CST)

输入还可以更好一点，比如只要是非中文的内容都应用美元号夹起来，题号可以不夹，不夹起来和夹起来的字体是不一样的，数学中是没有中文的句号，只能用英文的点号加上空格，但逗号中英文都有，但英文的逗号间距太小，所有要转换到中文状态下输。即逗号要用中文的，句号要用英文的。

-- Admin（留言） 2024年3月10日 (日) 13:53 (CST)

$\vec{n}=(1-\cos\theta,\sin\theta-2\cos\theta)$，我按这个讲

-- Admin（留言） 2024年3月10日 (日) 14:12 (CST)

视频讲解

-- Admin（留言） 2024年3月10日 (日) 15:44 (CST)

2024/3/15

123 Cyc（留言） 2024年3月15日 (五) 20:55 (CST)