7.3.2 离散型随机变量的方差:修订间差异
来自高中数学
(→知识要点) |
(→知识要点) |
||
| 第2行: | 第2行: | ||
==知识要点== | ==知识要点== | ||
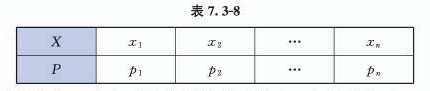
一般地,若离散型随机变量$X$的分布列如表7.3-2所示, | 一般地,若离散型随机变量$X$的分布列如表7.3-2所示, | ||
[[文件:2024040902.png]] | |||
则称$$D(X)=(x_1-E(X))^2p_1+(x_2-E(X))^2p_2+\cdots+(x_n-E(X))^2p_n$$即:$$D(X)=\sum_{i=1}^n(x_i-E(X))^2p_i$$ | 则称$$D(X)=(x_1-E(X))^2p_1+(x_2-E(X))^2p_2+\cdots+(x_n-E(X))^2p_n$$即:$$D(X)=\sum_{i=1}^n(x_i-E(X))^2p_i$$ | ||
2024年4月9日 (二) 18:47的版本
知识要点
一般地,若离散型随机变量$X$的分布列如表7.3-2所示,
则称$$D(X)=(x_1-E(X))^2p_1+(x_2-E(X))^2p_2+\cdots+(x_n-E(X))^2p_n$$即:$$D(X)=\sum_{i=1}^n(x_i-E(X))^2p_i$$ 为随机变量$X$的方差,并称$\sqrt{D(X)}$为随机变量$X$的标准差,记为$\sigma(X)$.
可以证明:
(1)$D(aX+b)=a^2D(X)$
(2)如果$X$服从两点分布,则$D(X)=p(1-p)$