讨论:8.4 空间点、直线、平面之间的位置关系:修订间差异
来自高中数学
最新留言:2024年5月17日 (星期五)由Cyc在话题2024/5/17内发布
无编辑摘要 |
|||
| 第1行: | 第1行: | ||
== 2024/4/19 == | == 2024/4/19 == | ||
[[文件:Cyc12.jpg|缩略图]] | |||
如图所示,在四棱锥P-ABCD,BC∥平面PAD,BC=$\dfrac{1}{2}$AD,E是PD中点 | 如图所示,在四棱锥P-ABCD,BC∥平面PAD,BC=$\dfrac{1}{2}$AD,E是PD中点 | ||
| 第10行: | 第11行: | ||
(3)若M是线段CE上一动点,则线段AD是否存在一点,使MN∥平面PAB?说明理由 | (3)若M是线段CE上一动点,则线段AD是否存在一点,使MN∥平面PAB?说明理由 | ||
| 第26行: | 第27行: | ||
== 2024/4/20 == | == 2024/4/20 == | ||
[[文件:Cyc13.jpg|缩略图]] | |||
如图,已知四棱锥P-ABCD的底面是菱形,AC交BD于点Q,E为AD中点F在PA上,AP=λAF,PC∥平面BEF,则λ的值为() | 如图,已知四棱锥P-ABCD的底面是菱形,AC交BD于点Q,E为AD中点F在PA上,AP=λAF,PC∥平面BEF,则λ的值为() | ||
| 第39行: | 第41行: | ||
2024年6月2日 (日) 09:58的版本
2024/4/19
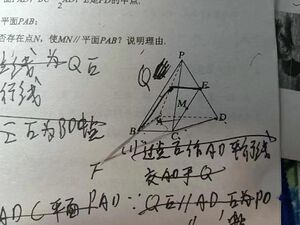
如图所示,在四棱锥P-ABCD,BC∥平面PAD,BC=$\dfrac{1}{2}$AD,E是PD中点
(1)求证:BC∥AD
(2)求证:CE∥平行PAB
(3)若M是线段CE上一动点,则线段AD是否存在一点,使MN∥平面PAB?说明理由
Cyc(留言) 2024年4月19日 (五) 21:00 (CST)
2024/4/20
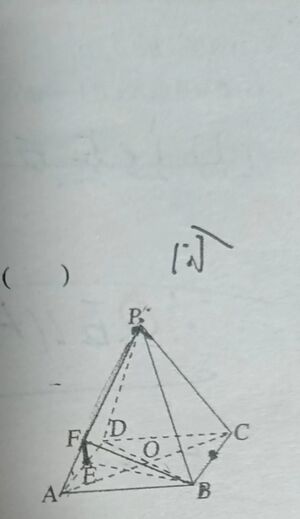
如图,已知四棱锥P-ABCD的底面是菱形,AC交BD于点Q,E为AD中点F在PA上,AP=λAF,PC∥平面BEF,则λ的值为()
A.1
B.$\dfrac{3}{2}$
C.3
D.2
Cyc(留言) 2024年4月20日 (六) 21:48 (CST)
2024/5/17
在正四面体S-ABC中,M是SC中点,N是SB中点,则异面直线BM与AN夹角的余弦值()
A.$\dfrac{1}{6}$
B.$\dfrac{1}{3}$
C.$\dfrac{\sqrt{3}}{2}$
D.$\dfrac{\sqrt{2}}{2}$
Cyc(留言) 2024年5月17日 (五) 22:34 (CST)