0804 空间直线、平面的垂直

知识要点

视频讲解

例题

1、2021新高考Ⅰ，20

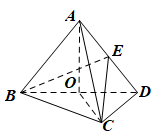
如图，在三棱锥$A-BCD$中，平面$ABD\perp$平面$BCD$，$AB=AD$，$O$为$BD$的中点.

（1）证明：$OA\perp CD$；

（2）若$\triangle OCD$是边长为1的等边三角形，点$E$在棱$AD$上，$DE=2EA$，且二面角$E-BC-D$的大小为$45^\circ$，求三棱锥$A-BCD$的体积.

答案 视频讲解

2、2022全国甲理，18

在四棱锥$P-ABCD$中，$PD\perp$底面$ABCD$，$CD\parallel AB$，$AD=DC=CB=1$，$AB=2$，$DP=\sqrt{3}$.

（1）证明：$BD\perp PA$；

（2）求$PD$与平面$PAB$所成角的正弦值.

答案 视频讲解

练习

1、2023全国甲理，11

已知四棱锥$P-ABCD$的底面是边长为4的正方形，$PC=PD=3$，$\angle PCA=45^\circ$，则$\triangle PBC$的面积为$(\qquad)$.

A. $2\sqrt{2}\qquad$B. $3\sqrt{2}\qquad$C. $4\sqrt{2}\qquad$D. $6\sqrt{2}\qquad$

答案

2、2023新课标，9

（多选）已知圆锥的顶点为$P$，底面圆心为$O$，$AB$为底面直径，$\angle APB=120^\circ$，$PA=2$，点$C$在底面圆周上，且二面角$P-AC-O$为$45^\circ$，则$(\qquad)$

A. 该圆锥的体积为$\pi$

B. 该圆锥的侧面积为$4\sqrt{3}\pi$

C. $AC=2\sqrt{2}$

D. $\triangle PAC$的面积为$\sqrt{3}$

答案

3、2023全国甲文，18

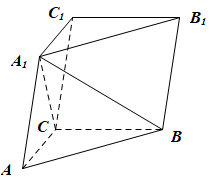
如图，在三棱柱$ABC-A_1B_1C_1$中，$A_1C\perp$平面$ABC$，$\angle ACB=90^\circ$.

（1）证明：平面$ACC_1A_1\perp$平面$BB_1C_1C$；

（2）设$AB=A_1B$，$AA_1=2$，求四棱锥$A_1-BB_1C_1C$的高.

答案

4、2021全国乙理，18

文件:2024052004.png

如图，在四棱锥$P-ABCD$中，$PD\perp$底面$ABCD$，$M$为$BC$的中点，且$PB\perp AM$.

（1）证明：平面$PAM\perp$平面$PBD$；

（2）若$PD=DC=1$，求四棱锥$P-ABCD$的体积.

答案