必修二问题讨论:修订间差异
来自高中数学
(→立几练习题) |
(→立几练习题) |
||
| 第6行: | 第6行: | ||
(2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积. | (2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积. | ||
===2、2019江苏,16=== | |||
[[文件:2024051403.png|缩略图|右]] | |||
如图,在直三棱柱$ABC-A_1B_1C_1$中,$D,E$分别是$BC,AC$的中点,$AB=BC$. 求证: | |||
(1)$A_1B_1\parallel$平面$DEC_1$; | |||
(2)$BE\perp C_1E$. | |||
[[category:必修第二册]] | [[category:必修第二册]] | ||
2024年8月2日 (五) 09:09的版本
立几练习题
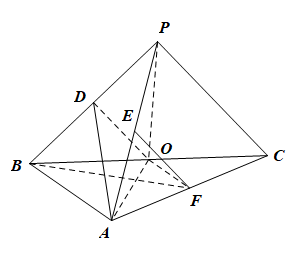
1. 如图,在三棱锥$P-ABC$中,$AB\perp BC$,$AB=2$,$BC=2\sqrt{2}$,$PB=PC=\sqrt{6}$,$BP,AP,BC$的中点分别为$D,E,O$,点$F$在$AC$上,$BF\perp AO$.
(1)证明:$EF\parallel$平面$ADO$;
(2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积.
2、2019江苏,16
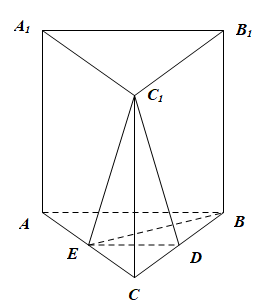
如图,在直三棱柱$ABC-A_1B_1C_1$中,$D,E$分别是$BC,AC$的中点,$AB=BC$. 求证:
(1)$A_1B_1\parallel$平面$DEC_1$;
(2)$BE\perp C_1E$.