讨论:平面向量及其应用复习:修订间差异
来自高中数学
最新留言:2024年3月10日 (星期日)由Admin在话题我有一个问题内发布
| 第11行: | 第11行: | ||
== 2024/03/10 == | == 2024/03/10 == | ||
[[文件:Cyc10.jpg|right|缩略图]] | |||
如图在所示平面直角坐标系中,已知点A(1,0)和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ,其中O为坐标原点 | 如图在所示平面直角坐标系中,已知点A(1,0)和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ,其中O为坐标原点 | ||
| 第19行: | 第19行: | ||
(2)θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值 | (2)θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值 | ||
2024年3月10日 (日) 12:39的版本
我有一个问题
这里是问题的描述。
--Admin(留言) 2024年3月3日 (日) 08:52 (CST)
- 现在开始回复,回复完了,记得换行,并输入两个减号--,两减号的意思是上面的话是谁说的。
- -- Admin(留言) 2024年3月10日 (日) 10:58 (CST)
2024/03/10
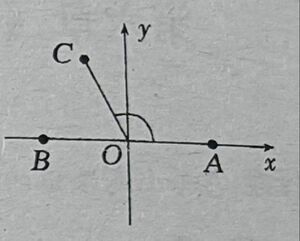
如图在所示平面直角坐标系中,已知点A(1,0)和点B(-1,0)$\overrightarrow{OC}$=1且$\angle$AOC=θ,其中O为坐标原点
(1)若θ=$\dfrac{3π}{4}$设点D为线段OA上的动点,求|$\overrightarrow{OC}$+$\overrightarrow{OD}$|的最小值
(2)θ$\in$[0,$\dfrac{π}{2}$],向量m=$\overrightarrow{BC}$,n=(1-cosθ,sinθ-cosθ)求m·n的的最小值及对应的θ值